Page 22 - Start Up Mathematics_8 (Non CCE)

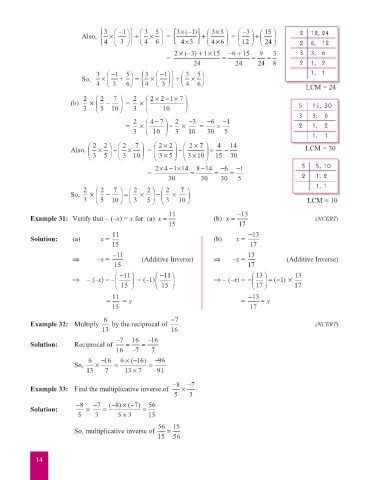
 3  − 1  3 5  { 3×−()  35×   3  15  2 12, 24
1
− 
+
Also,  ×   +  ×  = }   =   +  
×
 4  3   4 6  43×  46   12   24  2 6, 12
2 ×−( 3 +×) 115 −+ 9 3 3 3, 6
615
= = = =
24 24 24 8 2 1, 2
3  − 1 5  3  − 1   3 5 1, 1
So, ×  +  =  ×    +  × 
4  3 6  4  3    4 6 LCM = 24
2  2 7  2  22 17 
×− ×
(b) ×  −  = ×  
3  5 10  3  10  5 15, 30
3 3, 6
2  47−  2 − 3 −6 −1
= ×   = × = = 2 1, 2
3  10  3 10 30 5 1, 1
×
 2 2   2 7   22×   27  4 14
Also,  ×   ×  =     = − LCM = 30
−
−
×
 3 5   3 10   35×   310  15 30
×− ×
24 114 814− − 6 − 1 5 5, 10
= = = =
30 30 30 5 2 1, 2
1, 1
2  2 7   2 2   2 7 
−
=
So, ×  −   ×   × 
3  5 10   3 5   3 10  LCM = 10
11 −13
Example 31: Verify that – (–x) = x for: (a) x = (b) x = (NCERT)
15 17
11 −13
Solution: (a) x = (b) x =
15 17
−11 13
⇒ –x = (Additive Inverse) ⇒ –x = (Additive Inverse)
15 17
 −11   −11   13  13
⇒ – (–x) = –   = (–1)   ⇒ – (–x) = −   =−1() ×
 15   15   17  17
11 −13
= = x = = x
15 17

6 −7
Example 32: Multiply by the reciprocal of . (NCERT)
13 16
−7 16 −16
Solution: Reciprocal of = =
16 −7 7
6 − 16 6 ×−( 16) − 96
So, × = =
13 7 13 7× 91

−8 −7
Example 33: Find the multiplicative inverse of × .
5 3
−8 −7 ( −8) × −7( ) 56
Solution: × = =
5 3 53 15
×
56 15
So, multiplicative inverse of =
15 56

14