Page 153 - Start Up Mathematics_7

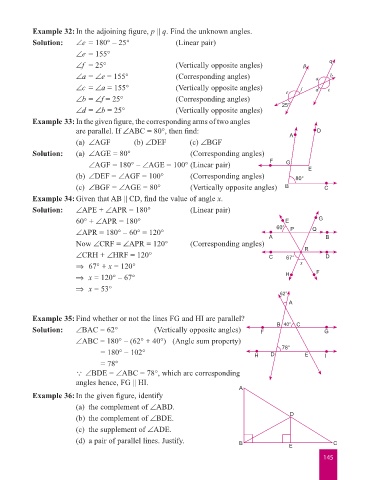
Example 32: In the adjoining figure, p || q. Find the unknown angles.

Solution: ∠e = 180° – 25° (Linear pair)
∠e = 155°
∠f = 25° (Vertically opposite angles) p q

∠a = ∠e = 155° (Corresponding angles) a b
∠c = ∠a = 155° (Vertically opposite angles) e f d c
∠b = ∠f = 25° (Corresponding angles)
25°
∠d = ∠b = 25° (Vertically opposite angles)
Example 33: In the given figure, the corresponding arms of two angles
are parallel. If ∠ABC = 80°, then find: D
A
(a) ∠AGF (b) ∠DEF (c) ∠BGF
Solution: (a) ∠AGE = 80° (Corresponding angles)

∠AGF = 180° – ∠AGE = 100° (Linear pair) F G
E
(b) ∠DEF = ∠AGF = 100° (Corresponding angles) 80°

(c) ∠BGF = ∠AGE = 80° (Vertically opposite angles) B C
Example 34: Given that AB || CD, find the value of angle x.
Solution: ∠APE + ∠APR = 180° (Linear pair)
60° + ∠APR = 180° E G
60° P Q
∠APR = 180° – 60° = 120° A B
Now ∠CRF = ∠APR = 120° (Corresponding angles)
R
∠CRH + ∠HRF = 120° C 67° D
⇒ 67° + x = 120° x
⇒ x = 120° – 67° H F
⇒ x = 53°
62°
A

Example 35: Find whether or not the lines FG and HI are parallel?
Solution: ∠BAC = 62° (Vertically opposite angles) F B 40° C G
∠ABC = 180° – (62° + 40°) (Angle sum property)

= 180° – 102° H D 78° E I
= 78°
 ∠BDE = ∠ABC = 78°, which are corresponding
angles hence, FG || HI.
A
Example 36: In the given figure, identify

(a) the complement of ∠ABD.
(b) the complement of ∠BDE. D

(c) the supplement of ∠ADE.
(d) a pair of parallel lines. Justify. B C
E

145