Page 290 - ICSE Math 8

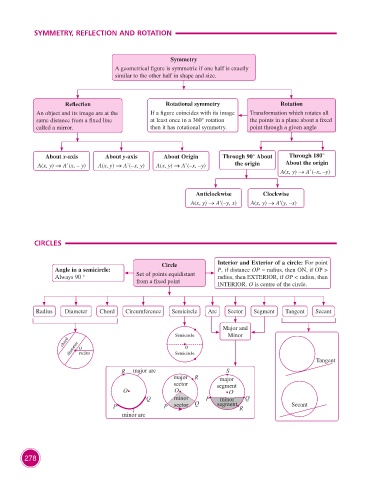
SYMMETRY, REFLECTION AND ROTATION

Symmetry
A geometrical figure is symmetric if one half is exactly
similar to the other half in shape and size.

Reflection Rotational symmetry Rotation
An object and its image are at the If a figure coincides with its image Transformation which rotates all
same distance from a fixed line at least once in a 360° rotation the points in a plane about a fixed
called a mirror. then it has rotational symmetry. point through a given angle

About x-axis About y-axis About Origin Through 90° About Through 180°
A(x, y) → A’(x, – y) A(x, y) → A’(–x, y) A(x, y) → A’(–x, –y) the origin About the origin
A(x, y) → A’(–x, –y)

Anticlockwise Clockwise
A(x, y) → A′(–y, x) A(x, y) → A′(y, –x)

CIRCLES

Circle Interior and Exterior of a circle: For point
Angle in a semicircle: P, if distance OP = radius, then ON, if >
Always 90 ° Set of points equidistant radius, then EXTERIOR, if OP < radius, then
from a fixed point INTERIOR. O is centre of the circle.

Radius Diameter Chord Circumference Semicircle Arc Sector Segment Tangent Secant

Major and
Semicircle Minor
chord
diameter O Semicircle
O
radius
Tangent

Secant

278