Page 287 - ICSE Math 8

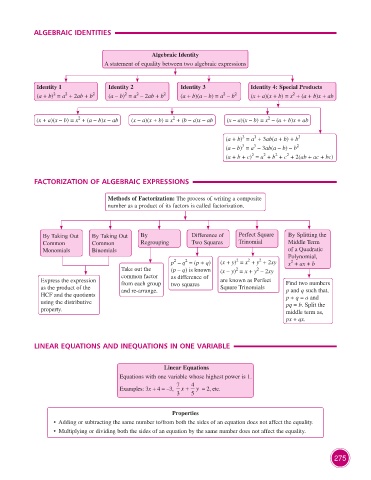
ALGEBRAIC IDENTITIES

Algebraic Identity
A statement of equality between two algebraic expressions

Identity 1 Identity 2 Identity 3 Identity 4: Special Products
2
2
2
2
2
2
(a + b) = a + 2ab + b 2 (a – b) = a – 2ab + b 2 (a + b)(a – b) = a – b 2 (x + a)(x + b) = x + (a + b)x + ab
2
2
2
(x + a)(x – b) = x + (a – b)x – ab (x – a)(x + b) = x + (b – a)x – ab (x – a)(x – b) = x – (a + b)x + ab
3
3
(a + b) = a + 3ab(a + b) + b 3
3
3
(a – b) = a – 3ab(a – b) – b 2
2
2
2
2
(a + b + c) = a + b + c + 2(ab + ac + bc)
FACTORIZATION OF ALGEBRAIC EXPRESSIONS
Methods of Factorization: The process of writing a composite
number as a product of its factors is called factorization.

By Taking Out By Taking Out By Difference of Perfect Square By Splitting the
Common Common Regrouping Two Squares Trinomial Middle Term
Monomials Binomials of a Quadratic
Polynomial,
2
2
2
2
2
2
p – q = (p + q) (x + y) = x + y + 2xy x + ax + b
Take out the (p – q) is known (x – y) = x + y – 2xy
2
2
common factor as difference of
Express the expression from each group are known as Perfect Find two numbers
as the product of the and re-arrange. two squares Square Trinomials p and q such that,
HCF and the quotients p + q = a and
using the distributive pq = b. Split the
property. middle term as,
px + qx.
LINEAR EQUATIONS AND INEQUATIONS IN ONE VARIABLE

Linear Equations
Equations with one variable whose highest power is 1.
7 4
Examples: 3x + 4 = –3, x + y = 2, etc.
3 5

Properties
• Adding or subtracting the same number to/from both the sides of an equation does not affect the equality.
• Multiplying or dividing both the sides of an equation by the same number does not affect the equality.

275