Page 288 - ICSE Math 8

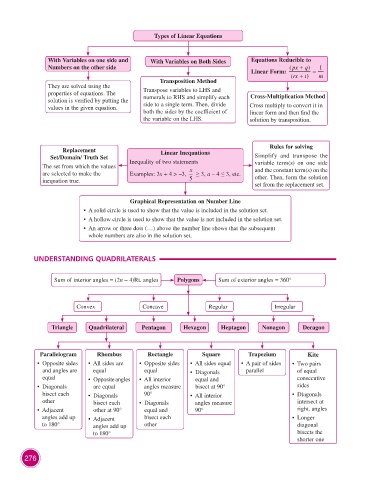
Types of Linear Equations

With Variables on one side and With Variables on Both Sides Equations Reducible to
Numbers on the other side ( px + ) q 1
Linear Form: (rx + ) t = m
Transposition Method
They are solved using the
properties of equations. The Transpose variables to LHS and Cross-Multiplication Method
solution is verified by putting the numerals to RHS and simplify each
values in the given equation. side to a single term. Then, divide Cross multiply to convert it in
both the sides by the coefficient of linear form and then find the
the variable on the LHS. solution by transposition.

Replacement Linear Inequations Rules for solving
Set/Domain/ Truth Set Inequality of two statements Simplify and transpose the
The set from which the values x variable term(s) on one side
and the constant term(s) on the
are selected to make the Examples: 3x + 4 > –3, ≥ 3, a – 4 ≤ 3, etc. other. Then, form the solution
inequation true. 5
set from the replacement set.

Graphical Representation on Number Line
• A solid circle is used to show that the value is included in the solution set.
• A hollow circle is used to show that the value is not included in the solution set.
• An arrow or three dots (…) above the number line shows that the subsequent
whole numbers are also in the solution set.

UNDERSTANDING QUADRILATERALS

Sum of interior angles = (2n – 4)Rt. angles Polygons Sum of exterior angles = 360°

Convex Concave Regular Irregular

Triangle Quadrilateral Pentagon Hexagon Heptagon Nonagon Decagon

Parallelogram Rhombus Rectangle Square Trapezium Kite
• Opposite sides • All sides are • Opposite sides • All sides equal • A pair of sides • Two pairs
and angles are equal equal • Diagonals parallel of equal
equal • Opposite angles • All interior equal and consecutive
• Diagonals are equal angles measure bisect at 90° sides
bisect each • Diagonals 90° • All interior • Diagonals
other bisect each • Diagonals angles measure intersect at
• Adjacent other at 90° equal and 90° right. angles
angles add up • Adjacent bisect each • Longer
to 180° angles add up other diagonal
to 180° bisects the
shorter one

276