Page 284 - ICSE Math 8

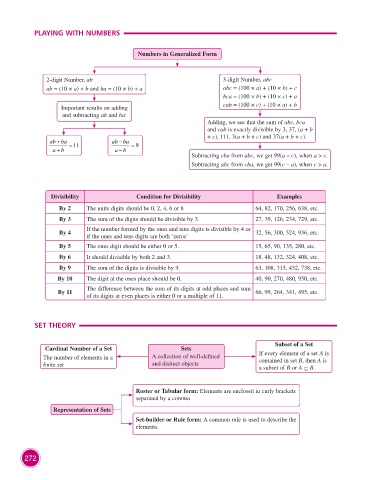
PLAYING WITH NUMBERS

Numbers in Generalized Form

2-digit Number, ab 3-digit Number, abc
ab = (10 × a) + b and ba = (10 × b) + a abc = (100 × a) + (10 × b) + c
bca = (100 × b) + (10 × c) + a
Important results on adding cab = (100 × c) + (10 × a) + b
and subtracting ab and ba:
Adding, we see that the sum of abc, bca
and cab is exactly divisible by 3, 37, (a + b
+ c), 111, 3(a + b + c) and 37(a + b + c).
−
ab + ba = 11 ab ba = 9
ab a b
−
+
Subtracting cba from abc, we get 99(a – c), when a > c.
Subtracting abc from cba, we get 99(c – a), when c > a.

Divisibility Condition for Divisibility Examples

By 2 The units digits should be 0, 2, 4, 6 or 8 64, 82, 170, 256, 638, etc.
By 3 The sum of the digits should be divisible by 3. 27, 39, 126, 234, 729, etc.
If the number formed by the ones and tens digits is divisible by 4 or
By 4 32, 56, 300, 524, 936, etc.
if the ones and tens digits are both ‘zeros’
By 5 The ones digit should be either 0 or 5. 15, 65, 90, 135, 280, etc.
By 6 It should divisible by both 2 and 3. 18, 48, 132, 324, 408, etc.
By 9 The sum of the digits is divisible by 9. 63, 108, 315, 432, 738, etc.

By 10 The digit at the ones place should be 0. 40, 90, 270, 480, 950, etc.
By 11 The difference between the sum of its digits at odd places and sum 66, 99, 264, 341, 495, etc.
of its digits at even places is either 0 or a multiple of 11.

SET THEORY

Subset of a Set
Cardinal Number of a Set Sets
The number of elements in a A collection of well-defined If every element of a set A is
contained in set B, then A is
finite set and distinct objects a subset of B or A ⊆ B.

Roster or Tabular form: Elements are enclosed in curly brackets
separated by a comma

Representation of Sets
Set-builder or Rule form: A common rule is used to describe the
elements.

272