Page 149 - ICSE Math 8

2
2
Identity 2: (a – b) = a – 2ab + b 2
In other words,
2
2
(Difference of the two terms) = (First term) – 2 ¥ (First term) ¥ (Second term) + (Second term) 2
2
Proof: (a – b) = (a – b)(a – b)
= a(a – b) – b(a – b) (Distributive property of multiplication over subtraction)
2
= a – ab – ab + b 2
2
= a – 2ab + b 2 (Commutative property ab = ba)
2
2
\ (a – b) = a – 2ab + b 2
Maths Info

2
2
(a + b) and (a – b) are known as perfect square trinomials. Any trinomials which can be expressed
2
2
2
2
in the form a + 2ab + b or a –2ab + b is known as a perfect square trinomial.
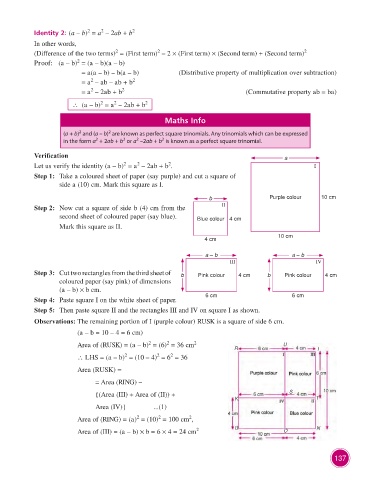
Verification a
2
2
2
Let us verify the identity (a – b) = a – 2ab + b . I
Step 1: Take a coloured sheet of paper (say purple) and cut a square of
side a (10) cm. Mark this square as I.
b Purple colour 10 cm
Step 2: Now cut a square of side b (4) cm from the II
second sheet of coloured paper (say blue). Blue colour 4 cm

Mark this square as II.
10 cm
4 cm

a – b a – b
III IV
Step 3: Cut two rectangles from the third sheet of b Pink colour 4 cm b Pink colour 4 cm
coloured paper (say pink) of dimensions
(a – b) ¥ b cm.
6 cm 6 cm
Step 4: Paste square I on the white sheet of paper.
Step 5: Then paste square II and the rectangles III and IV on square I as shown.
Observations: The remaining portion of I (purple colour) RUSK is a square of side 6 cm.

(a – b = 10 – 4 = 6 cm)
2
2
Area of (RUSK) = (a – b) = (6) = 36 cm 2 U
R I
2
2
2
\ LHS = (a – b) = (10 – 4) = 6 = 36
Area (RUSK) =
= Area (RING) –
{(Area (III) + Area of (II)) + S
K T
Area (IV)} ...(1)
2
2
2
Area of (RING) = (a) = (10) = 100 cm ,
Area of (III) = (a – b) ¥ b = 6 ¥ 4 = 24 cm 2 G O N

137