Page 342 - Start Up Mathematics_8 (Non CCE)

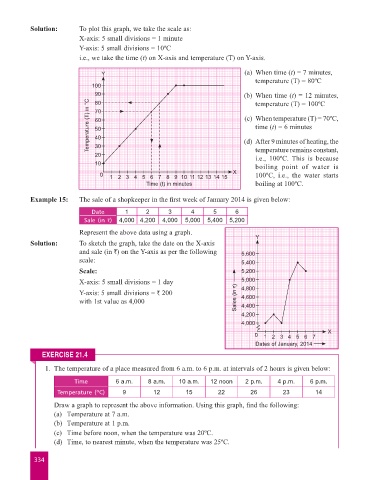
Solution: To plot this graph, we take the scale as:
X-axis: 5 small divisions = 1 minute
Y-axis: 5 small divisions = 10ºC
i.e., we take the time (t) on X-axis and temperature (T) on Y-axis.

Y (a) When time (t) = 7 minutes,
temperature (T) = 80ºC
100
90 (b) When time (t) = 12 minutes,
Temperature (T) in °C 50 time (t) = 6 minutes
80
temperature (T) = 100ºC
70 (c) When temperature (T) = 70ºC,
60

40 (d) After 9 minutes of heating, the
30
20 temperature remains constant,
i.e., 100ºC. This is because
10 boiling point of water is
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X 100ºC, i.e., the water starts
Time (t) in minutes boiling at 100ºC.

Example 15: The sale of a shopkeeper in the first week of January 2014 is given below:

Date 1 2 3 4 5 6
Sale (in `) 4,000 4,200 4,000 5,000 5,400 5,200
Represent the above data using a graph.
Y
Solution: To sketch the graph, take the date on the X-axis
and sale (in `) on the Y-axis as per the following 5,600
scale: 5,400
Scale: 5,200
X-axis: 5 small divisions = 1 day 5,000
Y-axis: 5 small divisions = ` 200 4,800
4,600
with 1st value as 4,000 Sales (in `) 4,400

4,200
4,000
X
0 1 2 3 4 5 6 7
Dates of January, 2014
EXERCISE 21.4

1. The temperature of a place measured from 6 a.m. to 6 p.m. at intervals of 2 hours is given below:
Time 6 a.m. 8 a.m. 10 a.m. 12 noon 2 p.m. 4 p.m. 6 p.m.

Temperature (ºC) 9 12 15 22 26 23 14
Draw a graph to represent the above information. Using this graph, find the following:
(a) Temperature at 7 a.m.
(b) Temperature at 1 p.m.
(c) Time before noon, when the temperature was 20ºC.
(d) Time, to nearest minute, when the temperature was 25ºC.

334