Page 257 - Start Up Mathematics_8 (Non CCE)

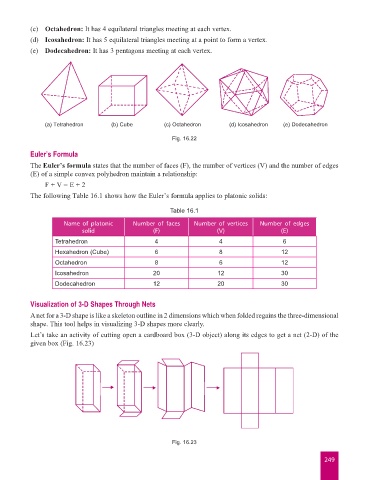
(c) Octahedron: It has 4 equilateral triangles meeting at each vertex.
(d) Icosahedron: It has 5 equilateral triangles meeting at a point to form a vertex.

(e) Dodecahedron: It has 3 pentagons meeting at each vertex.

(a) Tetrahedron (b) Cube (c) Octahedron (d) Icosahedron (e) Dodecahedron

Fig. 16.22

Euler’s Formula
The Euler’s formula states that the number of faces (F), the number of vertices (V) and the number of edges
(E) of a simple convex polyhedron maintain a relationship:
F + V = E + 2
The following Table 16.1 shows how the Euler’s formula applies to platonic solids:

Table 16.1
Name of platonic Number of faces Number of vertices Number of edges
solid (F) (V) (E)
Tetrahedron 4 4 6
Hexahedron (Cube) 6 8 12
Octahedron 8 6 12
Icosahedron 20 12 30
Dodecahedron 12 20 30

Visualization of 3-D Shapes Through Nets

A net for a 3-D shape is like a skeleton outline in 2 dimensions which when folded regains the three-dimensional
shape. This tool helps in visualizing 3-D shapes more clearly.

Let’s take an activity of cutting open a cardboard box (3-D object) along its edges to get a net (2-D) of the
given box (Fig. 16.23)

Fig. 16.23

249