Page 252 - Start Up Mathematics_8 (Non CCE)

16 Visualizing Shapes

In previous classes, you have learnt about various types of figures like one-dimensional,
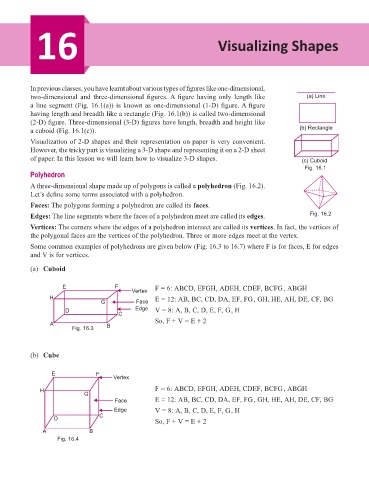
two-dimensional and three-dimensional figures. A figure having only length like (a) Line
a line segment (Fig. 16.1(a)) is known as one-dimensional (1-D) figure. A figure
having length and breadth like a rectangle (Fig. 16.1(b)) is called two-dimensional
(2-D) figure. Three-dimensional (3-D) figures have length, breadth and height like
a cuboid (Fig. 16.1(c)). (b) Rectangle
Visualization of 2-D shapes and their representation on paper is very convenient.
However, the tricky part is visualizing a 3-D shape and representing it on a 2-D sheet
of paper. In this lesson we will learn how to visualize 3-D shapes. (c) Cuboid
Fig. 16.1
Polyhedron
A three-dimensional shape made up of polygons is called a polyhedron (Fig. 16.2).
Let’s define some terms associated with a polyhedron.
Faces: The polygons forming a polyhedron are called its faces.
Edges: The line segments where the faces of a polyhedron meet are called its edges. Fig. 16.2

Vertices: The corners where the edges of a polyhedron intersect are called its vertices. In fact, the vertices of
the polygonal faces are the vertices of the polyhedron. Three or more edges meet at the vertex.

Some common examples of polyhedrons are given below (Fig. 16.3 to 16.7) where F is for faces, E for edges
and V is for vertices.

(a) Cuboid

E F F = 6: ABCD, EFGH, ADEH, CDEF, BCFG, ABGH
Vertex
H G Face E = 12: AB, BC, CD, DA, EF, FG, GH, HE, AH, DE, CF, BG
D Edge V = 8: A, B, C, D, E, F, G, H
C
A So, F + V = E + 2
Fig. 16.3 B

(b) Cube

E F
Vertex
H G F = 6: ABCD, EFGH, ADEH, CDEF, BCFG, ABGH
Face E = 12: AB, BC, CD, DA, EF, FG, GH, HE, AH, DE, CF, BG
C Edge V = 8: A, B, C, D, E, F, G, H
D So, F + V = E + 2

A B
Fig. 16.4