Page 253 - Start Up Mathematics_8 (Non CCE)

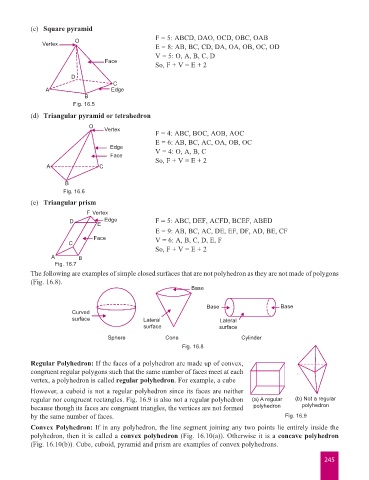
(c) Square pyramid
O F = 5: ABCD, DAO, OCD, OBC, OAB

Vertex E = 8: AB, BC, CD, DA, OA, OB, OC, OD
V = 5: O, A, B, C, D
Face So, F + V = E + 2
D
C
A Edge
B
Fig. 16.5
(d) Triangular pyramid or tetrahedron
O Vertex
F = 4: ABC, BOC, AOB, AOC
Edge E = 6: AB, BC, AC, OA, OB, OC
Face V = 4: O, A, B, C
So, F + V = E + 2
A C

B
Fig. 16.6
(e) Triangular prism
F Vertex
D E Edge F = 5: ABC, DEF, ACFD, BCEF, ABED

E = 9: AB, BC, AC, DE, EF, DF, AD, BE, CF
C Face V = 6: A, B, C, D, E, F
So, F + V = E + 2
A B
Fig. 16.7
The following are examples of simple closed surfaces that are not polyhedron as they are not made of polygons
(Fig. 16.8).
Base

Base Base
Curved
surface Lateral Lateral
surface surface

Sphere Cone Cylinder
Fig. 16.8

Regular Polyhedron: If the faces of a polyhedron are made up of convex,
congruent regular polygons such that the same number of faces meet at each
vertex, a polyhedron is called regular polyhedron. For example, a cube
However, a cuboid is not a regular polyhedron since its faces are neither
regular nor congruent rectangles. Fig. 16.9 is also not a regular polyhedron (a) A regular (b) Not a regular
because though its faces are congruent triangles, the vertices are not formed polyhedron polyhedron
by the same number of faces. Fig. 16.9

Convex Polyhedron: If in any polyhedron, the line segment joining any two points lie entirely inside the
polyhedron, then it is called a convex polyhedron (Fig. 16.10(a)). Otherwise it is a concave polyhedron
(Fig. 16.10(b)). Cube, cuboid, pyramid and prism are examples of convex polyhedrons.

245