Page 230 - Start Up Mathematics_8 (Non CCE)

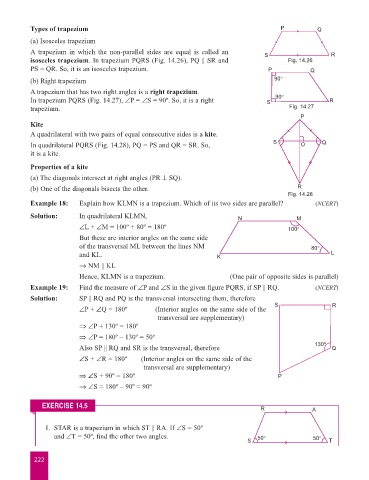
Types of trapezium P Q

(a) Isosceles trapezium
A trapezium in which the non-parallel sides are equal is called an S R
isosceles trapezium. In trapezium PQRS (Fig. 14.26), PQ || SR and Fig. 14.26
PS = QR. So, it is an isosceles trapezium. P Q

(b) Right trapezium 90°
A trapezium that has two right angles is a right trapezium.
In trapezium PQRS (Fig. 14.27), –P = –S = 90º. So, it is a right S 90° R
trapezium. Fig. 14.27
P
Kite
A quadrilateral with two pairs of equal consecutive sides is a kite.
In quadrilateral PQRS (Fig. 14.28), PQ = PS and QR = SR. So, S O Q
it is a kite.
Properties of a kite

(a) The diagonals intersect at right angles (PR ^ SQ).
(b) One of the diagonals bisects the other. R
Fig. 14.28
Example 18: Explain how KLMN is a trapezium. Which of its two sides are parallel? (NCERT)
Solution: In quadrilateral KLMN, N M

–L + –M = 100º + 80º = 180º 100°
But these are interior angles on the same side
of the transversal ML between the lines NM 80°
and KL. K L

fi NM || KL
Hence, KLMN is a trapezium. (One pair of opposite sides is parallel)
Example 19: Find the measure of –P and –S in the given figure PQRS, if SP || RQ. ( NCERT)
Solution: SP || RQ and PQ is the transversal intersecting them, therefore

–P + –Q = 180º ( Interior angles on the same side of the S R
transversal are supplementary)
fi –P + 130º = 180º
fi –P = 180º – 130º = 50º
Also SP || RQ and SR is the transversal, therefore 130º Q

–S + –R = 180º ( Interior angles on the same side of the
transversal are supplementary)
fi –S + 90º = 180º P
fi –S = 180º – 90º = 90º

EXERCISE 14.5 R A

1. STAR is a trapezium in which ST || RA. If ∠S = 50º
and ∠T = 50º, find the other two angles. 50° 50°
S T

222