Page 221 - Start Up Mathematics_8 (Non CCE)

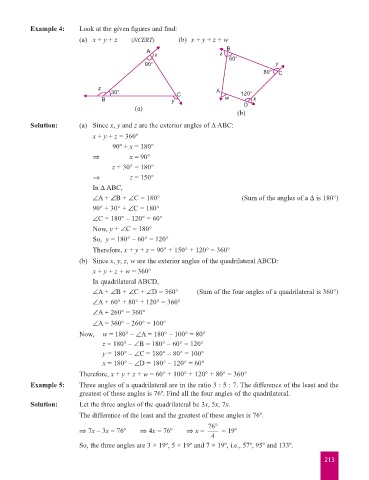
Example 4: Look at the given figures and find:
(a) x + y + z (NCERT) (b) x + y + z + w

A B
x z
60°
90° y
80° C

z
30° C A 120°
B y w D x
(a)
(b)

Solution: (a) Since x, y and z are the exterior angles of D ABC:
x + y + z = 360°
90º + x = 180°
fi x = 90°
z + 30° = 180°
fi z = 150°

In D ABC,
–A + –B + –C = 180° (Sum of the angles of a D is 180°)
90° + 30° + –C = 180°
–C = 180° – 120° = 60°
Now, y + –C = 180°
So, y = 180° – 60° = 120°
Therefore, x + y + z = 90° + 150° + 120° = 360°

(b) Since x, y, z, w are the exterior angles of the quadrilateral ABCD:
x + y + z + w = 360°
In quadrilateral ABCD,
–A + –B + –C + –D = 360° (Sum of the four angles of a quadrilateral is 360°)
–A + 60° + 80° + 120° = 360°
–A + 260° = 360°
–A = 360° – 260° = 100°
Now, w = 180° – –A = 180° – 100° = 80°
z = 180° – –B = 180° – 60° = 120°
y = 180° – –C = 180° – 80° = 100°
x = 180° – –D = 180° – 120° = 60°

Therefore, x + y + z + w = 60° + 100° + 120° + 80° = 360°
Example 5: Three angles of a quadrilateral are in the ratio 3 : 5 : 7. The difference of the least and the
greatest of these angles is 76º. Find all the four angles of the quadrilateral.
Solution: Let the three angles of the quadrilateral be 3x, 5x, 7x.
The difference of the least and the greatest of these angles is 76º.
76∞
fi 7x – 3x = 76º fi 4x = 76º fi x = = 19º
4
So, the three angles are 3 × 19º, 5 × 19º and 7 × 19º, i.e., 57º, 95º and 133º.

213