Page 195 - Start Up Mathematics_7

Example 21: In ∆ ABC, ∠A = 50°, ∠B = 20° and ∠C = 110°. In ∆ PQR, ∠P = 50°, ∠Q = 20°
and ∠R = 110°. A student says that ∆ ABC  ∆ PQR by AAA congruence criterion.
Is he justified? Why or why not?

Solution: ∆ ABC ∆ PQR, since AAA criterion for congruency does not exist. In fact, we
can have triangles of different sizes with the same corresponding angles.
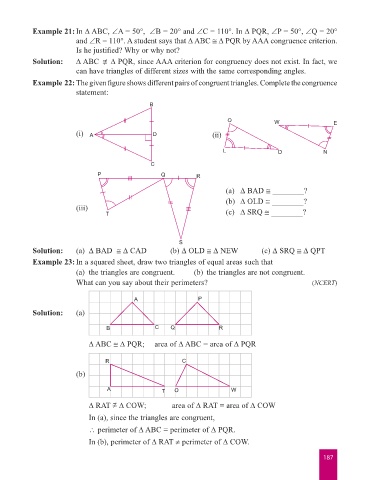
Example 22: The given figure shows different pairs of congruent triangles. Complete the congruence
statement:

B

O W E
(i) A D (ii)

L D N

C
P Q R

(a) ∆ BAD  ________?
(b) ∆ OLD  ________?
(iii)
T (c) ∆ SRQ  ________?

S
Solution: (a) ∆ BAD  ∆ CAD (b) ∆ OLD  ∆ NEW (c) ∆ SRQ  ∆ QPT

Example 23: In a squared sheet, draw two triangles of equal areas such that
(a) the triangles are congruent. (b) the triangles are not congruent.
What can you say about their perimeters? (NCERT)

A P
Solution: (a)

B C Q R

∆ ABC  ∆ PQR; area of ∆ ABC = area of ∆ PQR

R C
(b)

A T O W
∆ RAT ≅ ∆ COW; area of ∆ RAT = area of ∆ COW

In (a), since the triangles are congruent,

∴ perimeter of ∆ ABC = perimeter of ∆ PQR.
In (b), perimeter of ∆ RAT ≠ perimeter of ∆ COW.

187