Page 202 - Start Up Mathematics_7

Thinking Skills

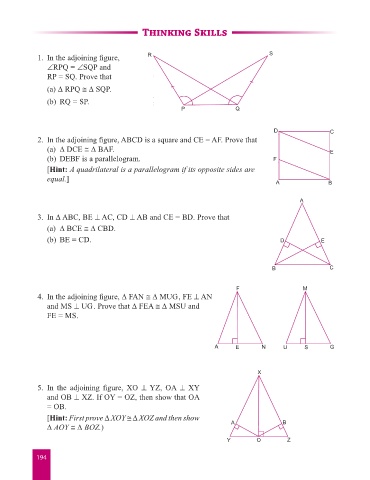
1. In the adjoining figure, R S
∠RPQ = ∠SQP and
RP = SQ. Prove that
(a) ∆ RPQ ≅ ∆ SQP.

(b) RQ = SP.
P Q

D C
2. In the adjoining figure, ABCD is a square and CE = AF. Prove that
(a) ∆ DCE ≅ ∆ BAF. E
(b) DEBF is a parallelogram. F
[Hint: A quadrilateral is a parallelogram if its opposite sides are
equal.]
A B

A

3. In ∆ ABC, BE ⊥ AC, CD ⊥ AB and CE = BD. Prove that
(a) ∆ BCE ≅ ∆ CBD.
(b) BE = CD. D E

B C

F M
4. In the adjoining figure, ∆ FAN ≅ ∆ MUG, FE ⊥ AN
and MS ⊥ UG. Prove that ∆ FEA ≅ ∆ MSU and
FE = MS.

A E N U S G

X

5. In the adjoining figure, XO ⊥ YZ, OA ⊥ XY
and OB ⊥ XZ. If OY = OZ, then show that OA
= OB.
[Hint: First prove ∆ XOY ≅ ∆ XOZ and then show
∆ AOY ≅ ∆ BOZ.) A B

Y O Z

194