Page 213 - ICSE Math 8

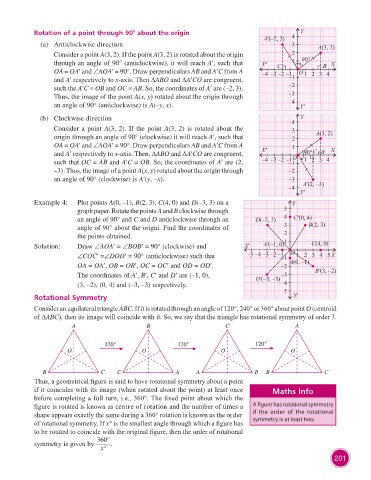
Rotation of a point through 90° about the origin

(a) Anticlockwise direction
Consider a point A(3, 2). If the point A(3, 2) is rotated about the origin
through an angle of 90° (anticlockwise), it will reach A′, such that
OA = OA′ and ∠AOA′ = 90°. Draw perpendiculars AB and A′C from A
and A′ respectively to x-axis. Then ∆ABO and ∆A′CO are congruent,
such the A′C = OB and OC = AB. So, the coordinates of A′ are (–2, 3).
Thus, the image of the point A(x, y) rotated about the origin through
an angle of 90° (anticlockwise) is A(–y, x).

(b) Clockwise direction
Consider a point A(3, 2). If the point A(3, 2) is rotated about the
origin through an angle of 90° (clockwise) it will reach A′, such that
OA = OA′ and ∠AOA′ = 90°. Draw perpendiculars AB and A′C from A
and A′ respectively to x-axis. Then, ∆ABO and ∆A′CO are congruent,
such that OC = AB and A′C = OB. So, the coordinates of A′ are (2,
–3). Thus, the image of a point A(x, y) rotated about the origin through
an angle of 90° (clockwise) is A′(y, –x).

Example 4: Plot points A(0, –1), B(2, 3), C(4, 0) and D(–3, 3) on a
graph paper. Rotate the points A and B clockwise through
an angle of 90° and C and D anticlockwise through an
angle of 90° about the origin. Find the coordinates of
the points obtained.

Solution: Draw ∠AOA′ = ∠BOB′ = 90° (clockwise) and
∠COC′ =∠DOD′ = 90° (anticlockwise) such that
OA = OA′, OB = OB′, OC = OC′ and OD = OD′.
The coordinates of A′, B′, C′ and D′ are (–1, 0),
(3, –2), (0, 4) and (–3, –3) respectively.
Rotational Symmetry

Consider an equilateral triangle ABC. If it is rotated through an angle of 120°, 240° or 360° about point O (centroid
of ∆ABC), then its image will coincide with it. So, we say that the triangle has rotational symmetry of order 3.
A B C A

120° 120° 120°
O O O O

B C C A A B B C
Thus, a geometrical figure is said to have rotational symmetry about a point
if it coincides with its image (when rotated about the point) at least once Maths Info
before completing a full turn, i.e., 360°. The fixed point about which the
figure is rotated is known as centre of rotation and the number of times a A figure has rotational symmetry
shape appears exactly the same during a 360° rotation is known as the order if the order of the rotational
symmetry is at least two.
of rotational symmetry. If x° is the smallest angle through which a figure has
to be rotated to coincide with the original figure, then the order of rotational
360°
symmetry is given by .
x°
201