Page 277 - Start Up Mathematics_8 (Non CCE)

Ê 1 ˜ { 1 } { 1 Ê 1 ˆ
ˆ
-
+
-
= Á 2 ¥¥ ¯ 2 ¥ ( 46 ¥) ( 73 ¥) 2 ¥ 6 ¥ ( 107 +) } Á Ë 2 ¥ 55¥ ˜ ¯
34 +
Ë
{ 1 } { 1 }
+ 2 ¥ 53( + ) ¥ 85( - ) ¥ 2 ¥ 10 8( - ) ¥ 3
Ê 1 ˆ Ê 1 ˆ Ê 1 ˆ Ê 1 ˆ Ê 1 ˆ Ê 1 ˆ
¥
23
34 +
63 +
55 +
= Á 2 ¥¥ ˜ Á 2 ¥ 10 4 + 2 ¥ ¥ ˜ ¯ Á 2 ¥ ¥ ˜ ¯ Á 2 ¥ 8 ¥ 33 + Á Ë 2 ¥ ¥ ˜ ¯
˜
˜ Á
¯
Ë
Ë
¯ Ë
¯ Ë
Ë
= 6 + 20 + 9 + 12.5 + 12 + 3 = 62.5 cm 2
2
\ Area of hexagon STRAIN = 62.5 cm .
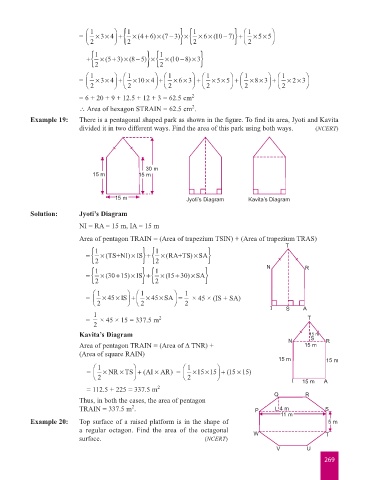
Example 19: There is a pentagonal shaped park as shown in the figure. To find its area, Jyoti and Kavita
divided it in two different ways. Find the area of this park using both ways. (NCERT)
30 m
15 m 15 m

15 m Jyoti’s Diagram Kavita’s Diagram

Solution: Jyoti’s Diagram
NI = RA = 15 m, IA = 15 m

Area of pentagon TRAIN = (Area of trapezium TSIN) + (Area of trapezium TRAS)
{ 1 } { 1 } T
= 2 ¥ (TS+NI ) ¥ IS + 2 ¥ (RA+TS ) ¥SA

{ 1 } { 1 } N R
¥
= 2 ¥ 30( +15) IS + 2 ¥ 15 30( + ) ) ¥SA
Ê 1 ˆ Ê 1 ˆ 1
+
= Á 2 ¥ 45 ¥ IS ˜ Á 2 ¥ 45 ¥SA ˜ ¯ = 2 × 45 × (IS + SA)
¯ Ë
Ë
I S A
1
= × 45 × 15 = 337.5 m 2 T
2
Kavita’s Diagram 15 m
N S R
Area of pentagon TRAIN = (Area of D TNR) + 15 m
(Area of square RAIN)
15 m 15 m
Ê 1 ˆ Ê 1 ˆ
¥
(
= Á ¥ NR TS ˜ + AI ¥ AR) = Á ¥ 15 15¥ ˜ + ( 15 15)
¥
¯
¯
Ë
Ë
2
2
I 15 m A
= 112.5 + 225 = 337.5 m 2
Q R
Thus, in both the cases, the area of pentagon
2
TRAIN = 337.5 m . P L 4 m S
11 m
Example 20: Top surface of a raised platform is in the shape of 5 m
a regular octagon. Find the area of the octagonal W
surface. (NCERT) T
V U
269