Page 124 - Start Up Mathematics_6

(b) Putting positive and negative terms in different brackets and adding them,
we get
(58 + 18) + {(–3) + ( –60) + (–20)} = 76 + {–(3 + 60 + 20)}

= 76 – 83 = –(83 – 76) = –7

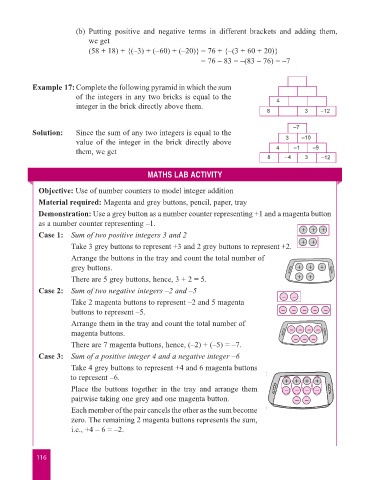
Example 17: Complete the following pyramid in which the sum
of the integers in any two bricks is equal to the 4
integer in the brick directly above them.
8 3 –12

–7
Solution: Since the sum of any two integers is equal to the
value of the integer in the brick directly above 3 –10
them, we get 4 –1 –9
8 –4 3 –12

MATHS LAB ACTIVITY

Objective: Use of number counters to model integer addition

Material required: Magenta and grey buttons, pencil, paper, tray
Demonstration: Use a grey button as a number counter representing +1 and a magenta button
as a number counter representing –1.
Case 1: Sum of two positive integers 3 and 2

Take 3 grey buttons to represent +3 and 2 grey buttons to represent +2.
Arrange the buttons in the tray and count the total number of
grey buttons.
There are 5 grey buttons, hence, 3 + 2 = 5.

Case 2: Sum of two negative integers –2 and –5
Take 2 magenta buttons to represent –2 and 5 magenta
buttons to represent –5.

Arrange them in the tray and count the total number of
magenta buttons.
There are 7 magenta buttons, hence, (–2) + (–5) = –7.
Case 3: Sum of a positive integer 4 and a negative integer –6

Take 4 grey buttons to represent +4 and 6 magenta buttons
to represent –6.
Place the buttons together in the tray and arrange them
pairwise taking one grey and one magenta button.

Each member of the pair cancels the other as the sum become
zero. The remaining 2 magenta buttons represents the sum,
i.e., +4 – 6 = –2.

116