Page 58 - Start Up Mathematics_5

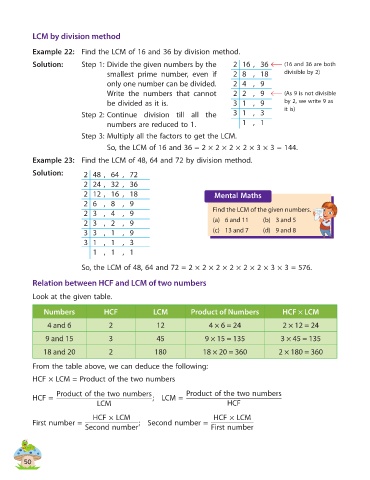
LCM by division method

Example 22: Find the LCM of 16 and 36 by division method.
Solution: Step 1: Divide the given numbers by the 2 16 , 36 (16 and 36 are both
smallest prime number, even if 2 8 , 18 divisible by 2)
only one number can be divided. 2 4 , 9
Write the numbers that cannot 2 2 , 9 (As 9 is not divisible
be divided as it is. 3 1 , 9 by 2, we write 9 as

Step 2: Continue division till all the 3 1 , 3 it is)
numbers are reduced to 1. 1 , 1
Step 3: Multiply all the factors to get the LCM.
So, the LCM of 16 and 36 = 2 × 2 × 2 × 2 × 3 × 3 = 144.

Example 23: Find the LCM of 48, 64 and 72 by division method.

Solution: 2 48 , 64 , 72
2 24 , 32 , 36
2 12 , 16 , 18 Mental Maths
2 6 , 8 , 9
2 3 , 4 , 9 Find the LCM of the given numbers.
2 3 , 2 , 9 (a) 6 and 11 (b) 3 and 5
3 3 , 1 , 9 (c) 13 and 7 (d) 9 and 8
3 1 , 1 , 3
1 , 1 , 1

So, the LCM of 48, 64 and 72 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 = 576.

Relation between HCF and LCM of two numbers

Look at the given table.

Numbers HCF LCM Product of Numbers HCF × LCM

4 and 6 2 12 4 × 6 = 24 2 × 12 = 24

9 and 15 3 45 9 × 15 = 135 3 × 45 = 135

18 and 20 2 180 18 × 20 = 360 2 × 180 = 360
From the table above, we can deduce the following:

HCF × LCM = Product of the two numbers

Product of the two numbers Product of the two numbers
HCF = ; LCM =
LCM HCF

HCF × LCM HCF × LCM
First number = ; Second number =
Second number First number

50