Page 7 - ICSE Math 8

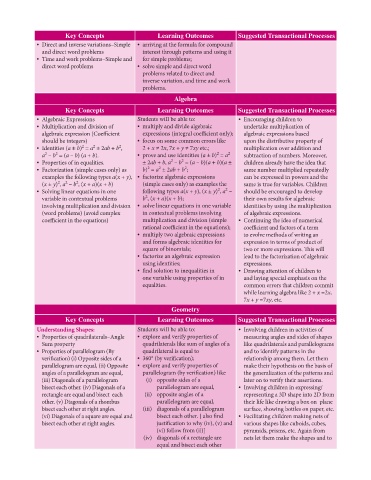
Key Concepts Learning Outcomes Suggested Transactional Processes
• Direct and inverse variations–Simple • arriving at the formula for compound
and direct word problems interest through patterns and using it
• Time and work problems–Simple and for simple problems;
direct word problems • solve simple and direct word
problems related to direct and
inverse variation, and time and work
problems.
Algebra
Key Concepts Learning Outcomes Suggested Transactional Processes
• Algebraic Expressions Students will be able to: • Encouraging children to
• Multiplication and division of • multiply and divide algebraic undertake multiplication of
algebraic expression (Coefficient expressions (integral coefficient only); algebraic expressions based
should be integers) • focus on some common errors like upon the distributive property of
2
2
2
• Identities (a ± b) = a ± 2ab + b , 2 + x ≠ 2x, 7x + y ≠ 7xy etc.; multiplication over addition and
2
2
2
2
a – b = (a – b) (a + b). • prove and use identities (a ± b) = a subtraction of numbers. Moreover,
2
2
• Properties of in equalities. ± 2ab + b, a – b = (a – b)(a + b)(a ± children already have the idea that
2
2
2
• Factorization (simple cases only) as b) = a ± 2ab + b ; same number multiplied repeatedly
examples the following types a(x + y), • factorize algebraic expressions can be expressed in powers and the
2
2
2
(x ± y) , a – b , (x + a)(x + b) (simple cases only) as examples the same is true for variables. Children
2
2
• Solving linear equations in one following types a(x + y), (x ± y) , a – should be encouraged to develop
2
variable in contextual problems b , (x + a)(x + b); their own results for algebraic
involving multiplication and division • solve linear equations in one variable identities by using the multiplication
(word problems) (avoid complex in contextual problems involving of algebraic expressions.
coefficient in the equations) multiplication and division (simple • Continuing the idea of numerical
rational coefficient in the equations); coefficient and factors of a term
• multiply two algebraic expressions to evolve methods of writing an
and forms algebraic identities for expression in terms of product of
square of binomials; two or more expressions. This will
• factorize an algebraic expression lead to the factorization of algebraic
using identities; expressions.
• find solution to inequalities in • Drawing attention of children to
one variable using properties of in and laying special emphasis on the
equalities. common errors that children commit
while learning algebra like 2 + x =2x,
7x + y =7xy, etc.
Geometry
Key Concepts Learning Outcomes Suggested Transactional Processes
Understanding Shapes: Students will be able to: • Involving children in activities of
• Properties of quadrilaterals–Angle • explore and verify properties of measuring angles and sides of shapes
Sum property quadrilaterals like sum of angles of a like quadrilaterals and parallelograms
• Properties of parallelogram (By quadrilateral is equal to and to identify patterns in the
verification) (i) Opposite sides of a • 360° (by verification); relationship among them. Let them
parallelogram are equal, (ii) Opposite • explore and verify properties of make their hypothesis on the basis of
angles of a parallelogram are equal, parallelogram (by verification) like the generalization of the patterns and
(iii) Diagonals of a parallelogram (i) opposite sides of a later on to verify their assertions.
bisect each other. (iv) Diagonals of a parallelogram are equal, • Involving children in expressing/
rectangle are equal and bisect each (ii) opposite angles of a representing a 3D shape into 2D from
other. (v) Diagonals of a rhombus parallelogram are equal, their life like drawing a box on plane
bisect each other at right angles. (iii) diagonals of a parallelogram surface, showing bottles on paper, etc.
(vi) Diagonals of a square are equal and bisect each other. [ also find • Facilitating children making nets of
bisect each other at right angles. justification to why (iv), (v) and various shapes like cuboids, cubes,
(vi) follow from (ii)] pyramids, prisms, etc. Again from
(iv) diagonals of a rectangle are nets let them make the shapes and to
equal and bisect each other