Page 253 - ICSE Math 8

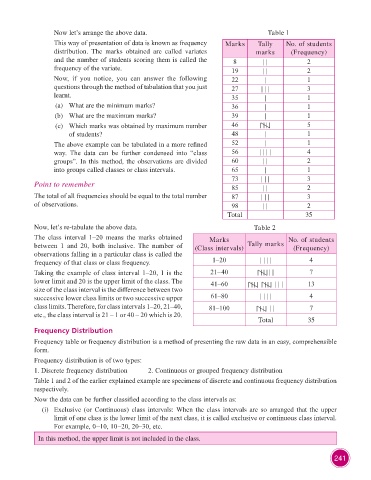
Now let’s arrange the above data. Table 1
This way of presentation of data is known as frequency Marks Tally No. of students
distribution. The marks obtained are called variates marks (Frequency)
and the number of students scoring them is called the 8 | | 2
frequency of the variate. 19 | | 2
Now, if you notice, you can answer the following 22 | 1
questions through the method of tabulation that you just 27 | | | 3
learnt. 35 | 1
(a) What are the minimum marks? 36 | 1

(b) What are the maximum marks? 39 | 1
(c) Which marks was obtained by maximum number 46 5
of students? 48 | 1

The above example can be tabulated in a more refined 52 | 1
way. The data can be further condensed into “class 56 | | | | 4
groups”. In this method, the observations are divided 60 | | 2
into groups called classes or class intervals. 65 | 1
73 | | | 3
Point to remember 85 | | 2
The total of all frequencies should be equal to the total number 87 | | | 3
of observations. 98 | | 2
Total 35

Now, let’s re-tabulate the above data. Table 2
The class interval 1–20 means the marks obtained Marks No. of students
between 1 and 20, both inclusive. The number of (Class intervals) Tally marks (Frequency)
observations falling in a particular class is called the
frequency of that class or class frequency. 1–20 | | | | 4
Taking the example of class interval 1–20, 1 is the 21–40 | | 7
lower limit and 20 is the upper limit of the class. The 41–60 | | | 13
size of the class interval is the difference between two
successive lower class limits or two successive upper 61–80 | | | | 4
class limits. Therefore, for class intervals 1–20, 21–40, 81–100 | | 7
etc., the class interval is 21 – 1 or 40 – 20 which is 20.
Total 35
Frequency Distribution
Frequency table or frequency distribution is a method of presenting the raw data in an easy, comprehensible
form.
Frequency distribution is of two types:
1. Discrete frequency distribution 2. Continuous or grouped frequency distribution

Table 1 and 2 of the earlier explained example are specimens of discrete and continuous frequency distribution
respectively.
Now the data can be further classified according to the class intervals as:

(i) Exclusive (or Continuous) class intervals: When the class intervals are so arranged that the upper
limit of one class is the lower limit of the next class, it is called exclusive or continuous class interval.
For example, 0–10, 10–20, 20–30, etc.

In this method, the upper limit is not included in the class.

241