Page 94 - Start Up Mathematics_8 (Non CCE)

3
2 2
3 2
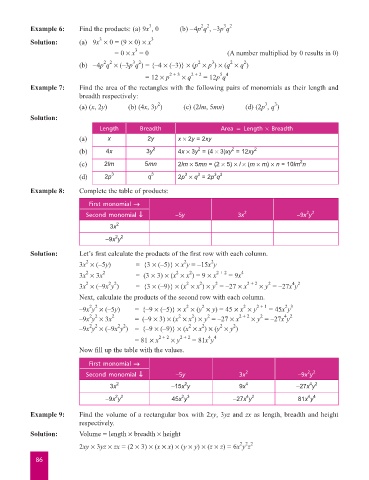
Example 6: Find the products: (a) 9x , 0 (b) –4p q , –3p q
3
Solution: (a) 9x ¥ 0 = (9 ¥ 0) ¥ x 3
3
= 0 ¥ x = 0 (A number multiplied by 0 results in 0)
2
2
2 2
3
2
3 2
(b) –4p q ¥ (–3p q ) = {–4 ¥ (–3)} ¥ (p ¥ p ) ¥ (q ¥ q )
5 4
= 12 ¥ p 2 + 3 ¥ q 2 + 2 = 12p q
Example 7: Find the area of the rectangles with the following pairs of monomials as their length and
breadth respectively:
3
2
3
(a) (x, 2y) (b) (4x, 3y ) (c) (2lm, 5mn) (d) (2p , q )
Solution:
Length Breadth Area = Length ¥ Breadth
(a) x 2y x ¥ 2y = 2xy
2
(b) 4x 3y 2 4x ¥ 3y = (4 ¥ 3)xy = 12xy 2
2
2
(c) 2lm 5mn 2lm ¥ 5mn = (2 ¥ 5) ¥ l ¥ (m ¥ m) ¥ n = 10lm n
3
3 3
3
(d) 2p 3 q 3 2p ¥ q = 2p q
Example 8: Complete the table of products:
First monomial Æ
2 2
Second monomial Ø –5y 3x 2 –9x y
3x 2
2 2
–9x y
Solution: Let’s first calculate the products of the first row with each column.
2
2
2
3x ¥ (–5y) = {3 ¥ (–5)} ¥ x y = –15x y
2
2
2
2
3x ¥ 3x = (3 ¥ 3) ¥ (x ¥ x ) = 9 ¥ x 2 + 2 = 9x 4
2
2
2
2
4 2
2 2
2
3x ¥ (–9x y ) = {3 ¥ (–9)} ¥ (x ¥ x ) ¥ y = –27 ¥ x 2 + 2 ¥ y = –27x y
Next, calculate the products of the second row with each column.
2
2 3
2
2 2
2
–9x y ¥ (–5y) = {–9 ¥ (–5)} ¥ x ¥ (y ¥ y) = 45 ¥ x ¥ y 2 + 1 = 45x y
2
2 2
2
4 2
2
2
2
–9x y ¥ 3x = (–9 ¥ 3) ¥ (x ¥ x ) ¥ y = –27 ¥ x 2 + 2 ¥ y = –27x y
2
2
2 2
2
2 2
2
–9x y ¥ (–9x y ) = {–9 ¥ (–9)} ¥ (x ¥ x ) ¥ (y ¥ y )
4 4
= 81 ¥ x 2 + 2 ¥ y 2 + 2 = 81x y
Now fill up the table with the values.
First monomial Æ
2 2
Second monomial Ø –5y 3x 2 –9x y
2
4 2
3x 2 –15x y 9x 4 –27x y
4 4
2 3
2 2
4 2
–9x y 45x y –27x y 81x y
Example 9: Find the volume of a rectangular box with 2xy, 3yz and zx as length, breadth and height
respectively.
Solution: Volume = length ¥ breadth ¥ height
2 2 2
2xy ¥ 3yz ¥ zx = (2 ¥ 3) ¥ (x ¥ x) ¥ (y ¥ y) ¥ (z ¥ z) = 6x y z
86