Page 56 - Start Up Mathematics_6

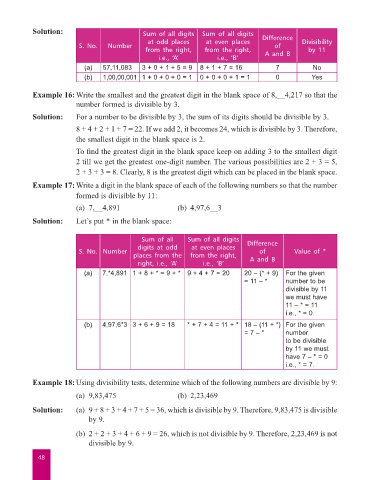
Solution: Sum of all digits Sum of all digits

at odd places at even places Difference Divisibility
S. No. Number of
from the right, from the right, by 11
i.e., ‘A’ i.e., ‘B’ A and B
(a) 57,11,083 3 + 0 + 1 + 5 = 9 8 + 1 + 7 = 16 7 No
(b) 1,00,00,001 1 + 0 + 0 + 0 = 1 0 + 0 + 0 + 1 = 1 0 Yes

Example 16: Write the smallest and the greatest digit in the blank space of 8,__4,217 so that the
number formed is divisible by 3.

Solution: For a number to be divisible by 3, the sum of its digits should be divisible by 3.

8 + 4 + 2 + 1 + 7 = 22. If we add 2, it becomes 24, which is divisible by 3. Therefore,
the smallest digit in the blank space is 2.
To find the greatest digit in the blank space keep on adding 3 to the smallest digit
2 till we get the greatest one-digit number. The various possibilities are 2 + 3 = 5,
2 + 3 + 3 = 8. Clearly, 8 is the greatest digit which can be placed in the blank space.

Example 17: Write a digit in the blank space of each of the following numbers so that the number
formed is divisible by 11:

(a) 7,__4,891 (b) 4,97,6__3
Solution: Let’s put * in the blank space:

Sum of all Sum of all digits Difference
digits at odd at even places
S. No. Number of Value of *
places from the from the right,
right, i.e., ‘A’ i.e., ‘B’ A and B
(a) 7,*4,891 1 + 8 + * = 9 + * 9 + 4 + 7 = 20 20 – (* + 9) For the given
= 11 – * number to be
divisible by 11
we must have
11 – * = 11
i.e., * = 0.
(b) 4,97,6*3 3 + 6 + 9 = 18 * + 7 + 4 = 11 + * 18 – (11 + *) For the given
= 7 – * number
to be divisible
by 11 we must
have 7 – * = 0
i.e., * = 7.

Example 18: Using divisibility tests, determine which of the following numbers are divisible by 9:
(a) 9,83,475 (b) 2,23,469

Solution: (a) 9 + 8 + 3 + 4 + 7 + 5 = 36, which is divisible by 9. Therefore, 9,83,475 is divisible
by 9.

(b) 2 + 2 + 3 + 4 + 6 + 9 = 26, which is not divisible by 9. Therefore, 2,23,469 is not
divisible by 9.

48