Page 55 - Start Up Mathematics_6

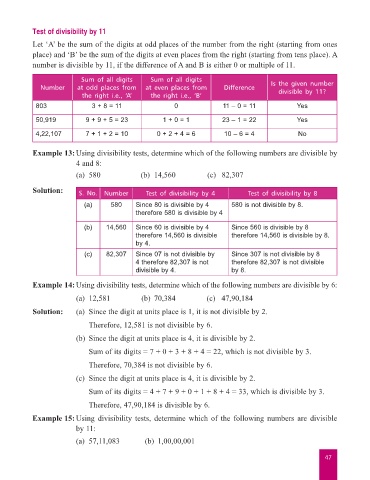
Test of divisibility by 11
Let ‘A’ be the sum of the digits at odd places of the number from the right (starting from ones
place) and ‘B’ be the sum of the digits at even places from the right (starting from tens place). A
number is divisible by 11, if the difference of A and B is either 0 or multiple of 11.

Sum of all digits Sum of all digits
Number at odd places from at even places from Difference Is the given number
the right i.e., ‘A’ the right i.e., ‘B’ divisible by 11?
803 3 + 8 = 11 0 11 – 0 = 11 Yes

50,919 9 + 9 + 5 = 23 1 + 0 = 1 23 – 1 = 22 Yes

4,22,107 7 + 1 + 2 = 10 0 + 2 + 4 = 6 10 – 6 = 4 No

Example 13: Using divisibility tests, determine which of the following numbers are divisible by

4 and 8:
(a) 580 (b) 14,560 (c) 82,307

Solution: S. No. Number Test of divisibility by 4 Test of divisibility by 8

(a) 580 Since 80 is divisible by 4 580 is not divisible by 8.
therefore 580 is divisible by 4

(b) 14,560 Since 60 is divisible by 4 Since 560 is divisible by 8
therefore 14,560 is divisible therefore 14,560 is divisible by 8.
by 4.

(c) 82,307 Since 07 is not divisible by Since 307 is not divisible by 8
4 therefore 82,307 is not therefore 82,307 is not divisible
divisible by 4. by 8.

Example 14: Using divisibility tests, determine which of the following numbers are divisible by 6:
(a) 12,581 (b) 70,384 (c) 47,90,184

Solution: (a) Since the digit at units place is 1, it is not divisible by 2.

Therefore, 12,581 is not divisible by 6.

(b) Since the digit at units place is 4, it is divisible by 2.
Sum of its digits = 7 + 0 + 3 + 8 + 4 = 22, which is not divisible by 3.

Therefore, 70,384 is not divisible by 6.

(c) Since the digit at units place is 4, it is divisible by 2.

Sum of its digits = 4 + 7 + 9 + 0 + 1 + 8 + 4 = 33, which is divisible by 3.
Therefore, 47,90,184 is divisible by 6.

Example 15: Using divisibility tests, determine which of the following numbers are divisible
by 11:

(a) 57,11,083 (b) 1,00,00,001

47