Page 202 - ICSE Math 8

D¢ C¢
O¢
A¢ B¢
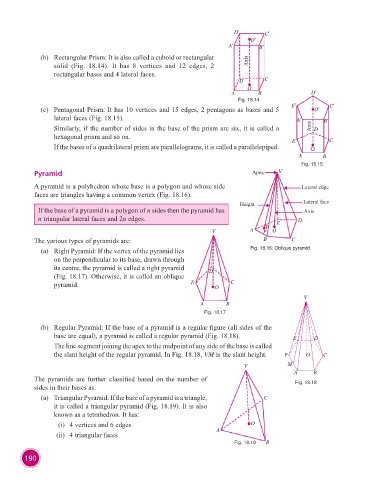
(b) Rectangular Prism: It is also called a cuboid or rectangular Axis
solid (Fig. 18.14). It has 8 vertices and 12 edges, 2
rectangular bases and 4 lateral faces.
D C
O
A B D¢
Fig. 18.14
E¢ C¢
(c) Pentagonal Prism: It has 10 vertices and 15 edges, 2 pentagons as bases and 5 O¢
lateral faces (Fig. 18.15). A¢ B¢
Similarly, if the number of sides in the base of the prism are six, it is called a Axis D
hexagonal prism and so on. E C
If the bases of a quadrilateral prism are parallelograms, it is called a parallelepiped. O
A B
Fig. 18.15
Pyramid Apex V
A pyramid is a polyhedron whose base is a polygon and whose side Lateral edge
faces are triangles having a common vertex (Fig. 18.16).
Height Lateral face
If the base of a pyramid is a polygon of n sides then the pyramid has Axis
n triangular lateral faces and 2n edges. D
E
V A P O
The various types of pyramids are: B C
(a) Right Pyramid: If the vertex of the pyramid lies Fig. 18.16: Oblique pyramid
on the perpendicular to its base, drawn through
its centre, the pyramid is called a right pyramid D
(Fig. 18.17). Otherwise, it is called an oblique
pyramid. E O C

V
A B
Fig. 18.17

(b) Regular Pyramid: If the base of a pyramid is a regular figure (all sides of the
base are equal), a pyramid is called a regular pyramid (Fig. 18.18). E D
The line segment joining the apex to the midpoint of any side of the base is called
the slant height of the regular pyramid. In Fig. 18.18, VM is the slant height. F O C

V M
A B
The pyramids are further classified based on the number of Fig. 18.18
sides in their bases as:
(a) Triangular Pyramid: If the base of a pyramid is a triangle, C
it is called a triangular pyramid (Fig. 18.19). It is also
known as a tetrahedron. It has:
(i) 4 vertices and 6 edges O
(ii) 4 triangular faces A
Fig. 18.19 B

190