Page 286 - Start Up Mathematics_8 (Non CCE)

Internal depth of tank = (110 – 3.5) cm = 106.5 cm
Internal volume of tank = 218 cm × 205 cm × 106.5 cm = 47,59,485 cm 3

Volume of iron used = External volume – Internal volume
3
= (52,47,000 – 47,59,485) cm = 4,87,515 cm 3
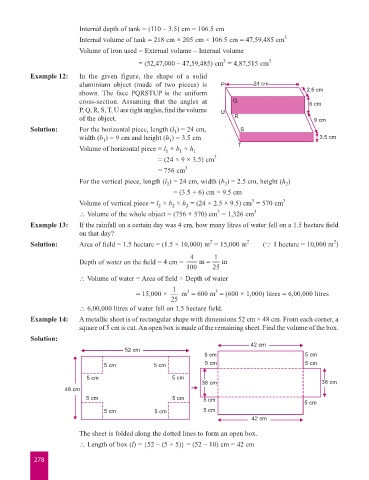
Example 12: In the given figure, the shape of a solid
aluminium object (made of two pieces) is P 24 cm
shown. The face PQRSTUP is the uniform 2.5 cm
cross-section. Assuming that the angles at Q 6 cm
P, Q, R, S, T, U are right angles, find the volume U
of the object. R 9 cm

Solution: For the horizontal piece, length (l ) = 24 cm, S
1
width (b ) = 9 cm and height (h ) = 3.5 cm 3.5 cm
1
1
Volume of horizontal piece = l × b × h T
1
1
1
= (24 × 9 × 3.5) cm 3
= 756 cm 3
For the vertical piece, length (l ) = 24 cm, width (b ) = 2.5 cm, height (h )
2
2
2
= (3.5 + 6) cm = 9.5 cm
3
Volume of vertical piece = l × b × h = (24 × 2.5 × 9.5) cm = 570 cm 3
2
2
2
3
\ Volume of the whole object = (756 + 570) cm = 1,326 cm 3
Example 13: If the rainfall on a certain day was 4 cm, how many litres of water fell on a 1.5 hectare field
on that day?
2
2
Solution: Area of field = 1.5 hectare = (1.5 × 10,000) m = 15,000 m 2 (  1 hectare = 10,000 m )
4 1
Depth of water on the field = 4 cm = m = m
100 25
\ Volume of water = Area of field × Depth of water
1
3
3
= 15,000 × m = 600 m = (600 × 1,000) litres = 6,00,000 litres
25
\ 6,00,000 litres of water fell on 1.5 hectare field.
Example 14: A metallic sheet is of rectangular shape with dimensions 52 cm × 48 cm. From each corner, a
square of 5 cm is cut. An open box is made of the remaining sheet. Find the volume of the box.

Solution:
42 cm
52 cm
5 cm 5 cm
5 cm 5 cm 5 cm 5 cm

5 cm 5 cm
38 cm 38 cm
48 cm
5 cm 5 cm 5 cm 5 cm
5 cm 5 cm 5 cm
42 cm

The sheet is folded along the dotted lines to form an open box.
\ Length of box (l) = {52 – (5 + 5)} = (52 – 10) cm = 42 cm

278