Page 333 - Start Up Mathematics_7

Additional Maths Lab Activities

Tesellations

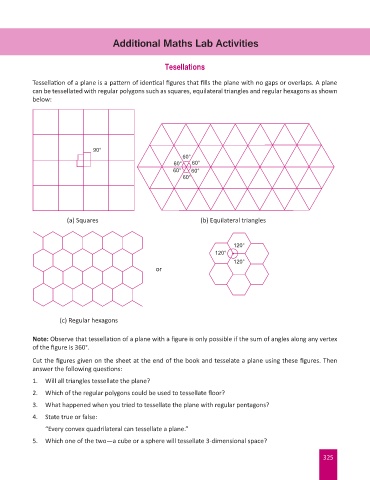
Tessellation of a plane is a pattern of identical figures that fills the plane with no gaps or overlaps. A plane
can be tessellated with regular polygons such as squares, equilateral triangles and regular hexagons as shown
below:

90°
60°
60° 60°
60° 60°
60°

(a) Squares (b) Equilateral triangles

120°
120°
120°
or

(c) Regular hexagons

Note: Observe that tessellation of a plane with a figure is only possible if the sum of angles along any vertex
of the figure is 360°.
Cut the figures given on the sheet at the end of the book and tesselate a plane using these figures. Then
answer the following questions:

1. Will all triangles tessellate the plane?
2. Which of the regular polygons could be used to tessellate floor?

3. What happened when you tried to tessellate the plane with regular pentagons?
4. State true or false:

“Every convex quadrilateral can tessellate a plane.”
5. Which one of the two—a cube or a sphere will tessellate 3-dimensional space?

325