Page 307 - Start Up Mathematics_7

Project Work

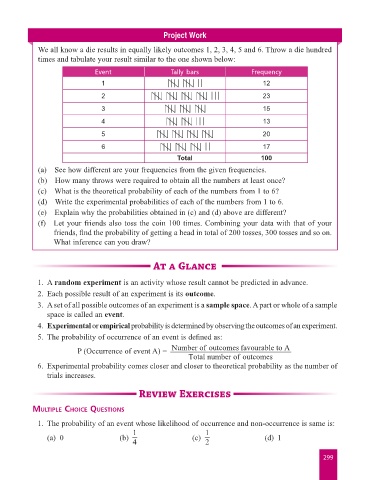
We all know a die results in equally likely outcomes 1, 2, 3, 4, 5 and 6. Throw a die hundred
times and tabulate your result similar to the one shown below:

Event Tally bars Frequency
1 12

2 23

3 15
4 13

5 20
6 17

Total 100
(a) See how different are your frequencies from the given frequencies.
(b) How many throws were required to obtain all the numbers at least once?
(c) What is the theoretical probability of each of the numbers from 1 to 6?
(d) Write the experimental probabilities of each of the numbers from 1 to 6.

(e) Explain why the probabilities obtained in (c) and (d) above are different?
(f) Let your friends also toss the coin 100 times. Combining your data with that of your
friends, find the probability of getting a head in total of 200 tosses, 300 tosses and so on.
What inference can you draw?

At a Glance

1. A random experiment is an activity whose result cannot be predicted in advance.

2. Each possible result of an experiment is its outcome.
3. A set of all possible outcomes of an experiment is a sample space. A part or whole of a sample
space is called an event.
4. Experimental or empirical probability is determined by observing the outcomes of an experiment.
5. The probability of occurrence of an event is defined as:

P (Occurrence of event A) = Number of outcomes favourable to A
Total number of outcomes
6. Experimental probability comes closer and closer to theoretical probability as the number of
trials increases.

Review Exercises

Multiple ChoiCe Questions
1. The probability of an event whose likelihood of occurrence and non-occurrence is same is:
1 1
(a) 0 (b) (c) (d) 1
4 2

299