Page 252 - Start Up Mathematics_7

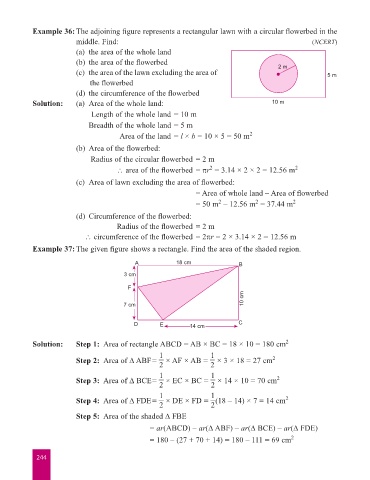
Example 36: The adjoining figure represents a rectangular lawn with a circular flowerbed in the

middle. Find: (NCERT)
(a) the area of the whole land
(b) the area of the flowerbed 2 m
(c) the area of the lawn excluding the area of 5 m
the flowerbed
(d) the circumference of the flowerbed
Solution: (a) Area of the whole land: 10 m
Length of the whole land = 10 m

Breadth of the whole land = 5 m
Area of the land = l × b = 10 × 5 = 50 m 2

(b) Area of the flowerbed:
Radius of the circular flowerbed = 2 m
2
∴ area of the flowerbed = πr = 3.14 × 2 × 2 = 12.56 m 2
(c) Area of lawn excluding the area of flowerbed:

= Area of whole land – Area of flowerbed
2
2
= 50 m – 12.56 m = 37.44 m 2
(d) Circumference of the flowerbed:
Radius of the flowerbed = 2 m
∴ circumference of the flowerbed = 2πr = 2 × 3.14 × 2 = 12.56 m
Example 37: The given figure shows a rectangle. Find the area of the shaded region.

A 18 cm B
3 cm

F
10 cm
7 cm

D E 14 cm C

Solution: Step 1: Area of rectangle ABCD = AB × BC = 18 × 10 = 180 cm 2
1 1
Step 2: Area of ∆ ABF = × AF × AB = × 3 × 18 = 27 cm 2
2 2
1 1
Step 3: Area of ∆ BCE = × EC × BC = × 14 × 10 = 70 cm 2
2 2
1 1
Step 4: Area of ∆ FDE = × DE × FD = (18 – 14) × 7 = 14 cm 2
2 2
Step 5: Area of the shaded ∆ FBE
= ar(ABCD) – ar(∆ ABF) – ar(∆ BCE) – ar(∆ FDE)

= 180 – (27 + 70 + 14) = 180 – 111 = 69 cm 2

244