Page 129 - Start Up Mathematics_7

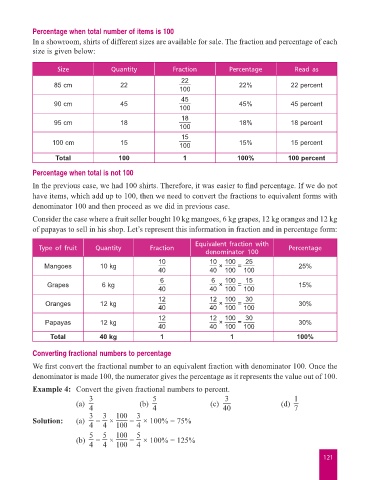
Percentage when total number of items is 100
In a showroom, shirts of different sizes are available for sale. The fraction and percentage of each
size is given below:

Size Quantity Fraction Percentage Read as

22
85 cm 22 22% 22 percent
100
45
90 cm 45 45% 45 percent
100
18
95 cm 18 18% 18 percent
100
15
100 cm 15 100 15% 15 percent

Total 100 1 100% 100 percent

Percentage when total is not 100
In the previous case, we had 100 shirts. Therefore, it was easier to find percentage. If we do not
have items, which add up to 100, then we need to convert the fractions to equivalent forms with
denominator 100 and then proceed as we did in previous case.

Consider the case where a fruit seller bought 10 kg mangoes, 6 kg grapes, 12 kg oranges and 12 kg
of papayas to sell in his shop. Let’s represent this information in fraction and in percentage form:

Equivalent fraction with
Type of fruit Quantity Fraction Percentage
denominator 100
10 10 100 25
Mangoes 10 kg × = 25%
40 40 100 100
6 6 100 15
Grapes 6 kg × = 15%
40 40 100 100
12 12 100 30
Oranges 12 kg × = 30%
40 40 100 100
12 12 100 30
Papayas 12 kg × = 30%
40 40 100 100
Total 40 kg 1 1 100%

Converting fractional numbers to percentage
We first convert the fractional number to an equivalent fraction with denominator 100. Once the
denominator is made 100, the numerator gives the percentage as it represents the value out of 100.

Example 4: Convert the given fractional numbers to percent.
3 5 3 1
(a) (b) (c) (d)
4 4 40 7
3
3
Solution: (a) 3 = × 100 = × 100% = 75%
4 4 100 4
5 5 100 5
(b) = × = × 100% = 125%
4 4 100 4

121